Корзина пуста
Анализ радиолокационных сигналов с демодуляцией
Анализ радиолокационных сигналов с демодуляцией
http://blog.teledynelecroy.com/2015/11/analyzing-radar-signals-with.html class=l>Оригинал статьи (eng.)
Перевод с англ. Карданец С.Г.
Современные осциллографы обладают широким набором математических функций, которые могут применяться для исследования сложных радиочастотных сигналов. Рассмотрим такую математическую функцию как демодуляция, применительно к исследованию радиолокационных сигналов. Радар использует радиочастотную энергию, чтобы определить радиус, угол и скорость движения объектов. В таких системах необходимо проводить измерения и анализ модулированных сигналов в полосе частот до нескольких гигагерц, спектр которых меняется во времени. Поэтому в анализе радарных сигналов бывает очень полезно использование математической функции осциллографа – демодуляции. Рассмотрим несколько примеров использования таких измерений.
Для начала - импульсный сигнал радара с несущей частотой 1 ГГц (рис. 1).
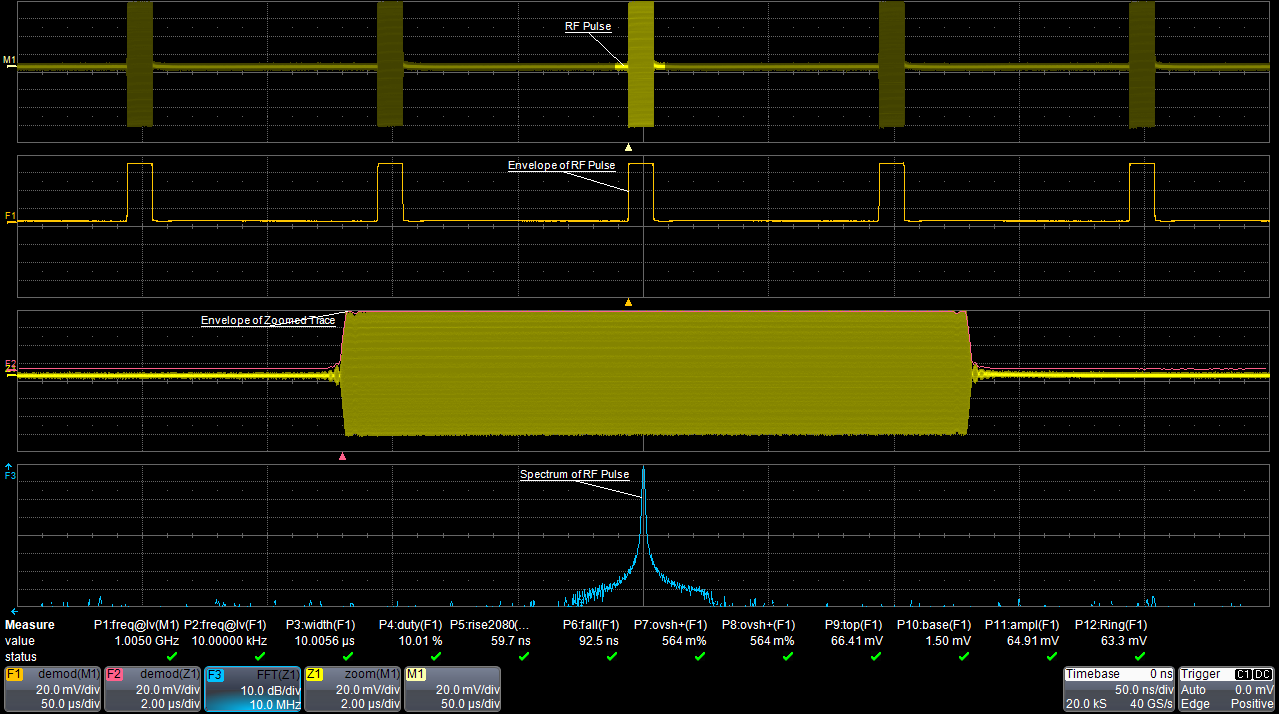 |
Рисунок 1. Пример радиолокационного сигнала с несущей частотой 1 ГГц |
В этом примере используются несколько математических операторов. Один из них - демодуляция входящего радиосигнала (математическая функция F1), который выделяет огибающую амплитудно-модулированного сигнала на входе. Другой математический оператор демодуляции применяется для масштабирования осциллограммы (математическая функция F2), наложенного на функцию увеличения (Z1). Осциллограмма Z1 отображает один радио-частотный импульс от входного сигнала. Наконец, в нижней части экрана отображается функция быстрого преобразования Фурье (БПФ) от масштабируемого сигнала (математическая функция F3), показывающая частотные составляющие этого импульса.
В нижней экрана отображается массив измерений демодулированного импульса, включая несущую и частоту модуляции, длительность, скважность, время нарастания/спада, превышения и амплитуды. Это - часть информации, которая может быть извлечена из радиочастотного сигнала, сразу после его демодуляции.
Другой пример радиолокационного сигнала является кодировка Баркера, в котором используется фазовая модуляция вместо амплитудной модуляции (рис. 2).
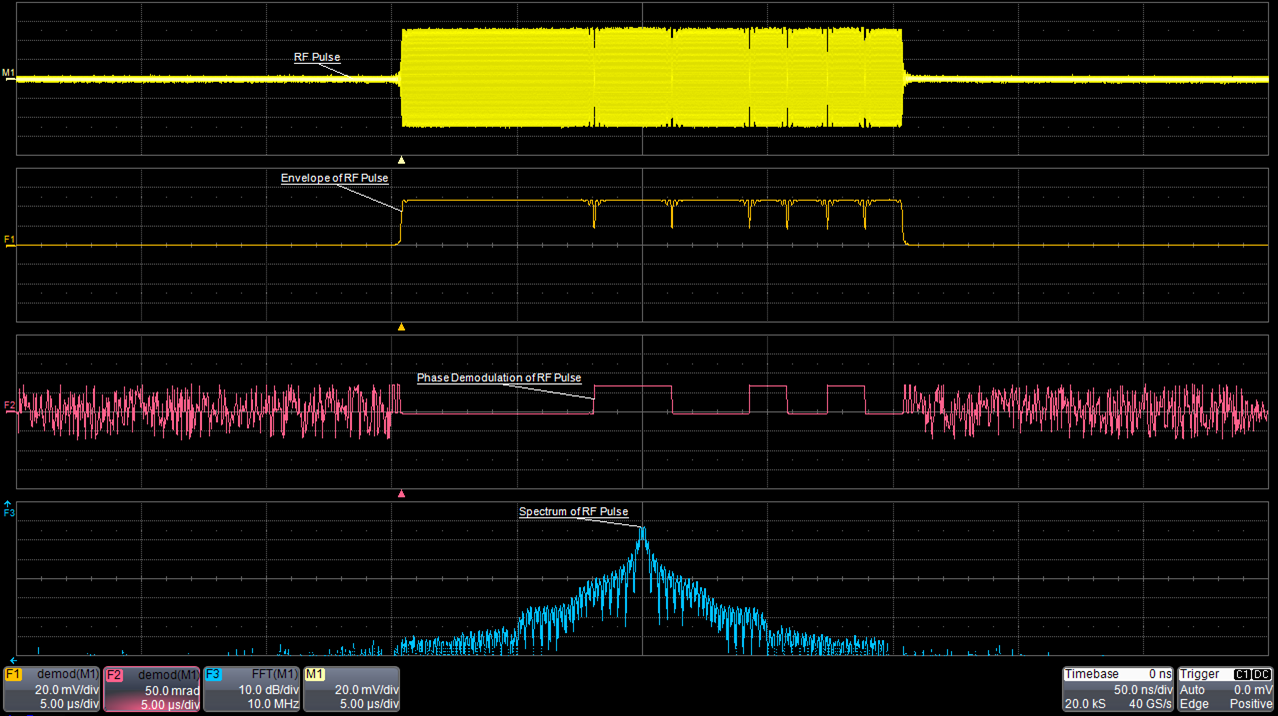 |
Рисунок 2. Пример радиолокационного сигнала в кодировке Баркера |
Это похоже по форме на радиолокационный сигнал с амплитудной модуляцией из предыдущего примера, но в этом случае мы используем математический оператор демодуляции для получения огибающей фазомодулированного сигнала. Демодулированный сигнал ясно показывает кодировку Баркера. В нижней части рисунка отображается частотный спектр сигнала (математическая функция F3).
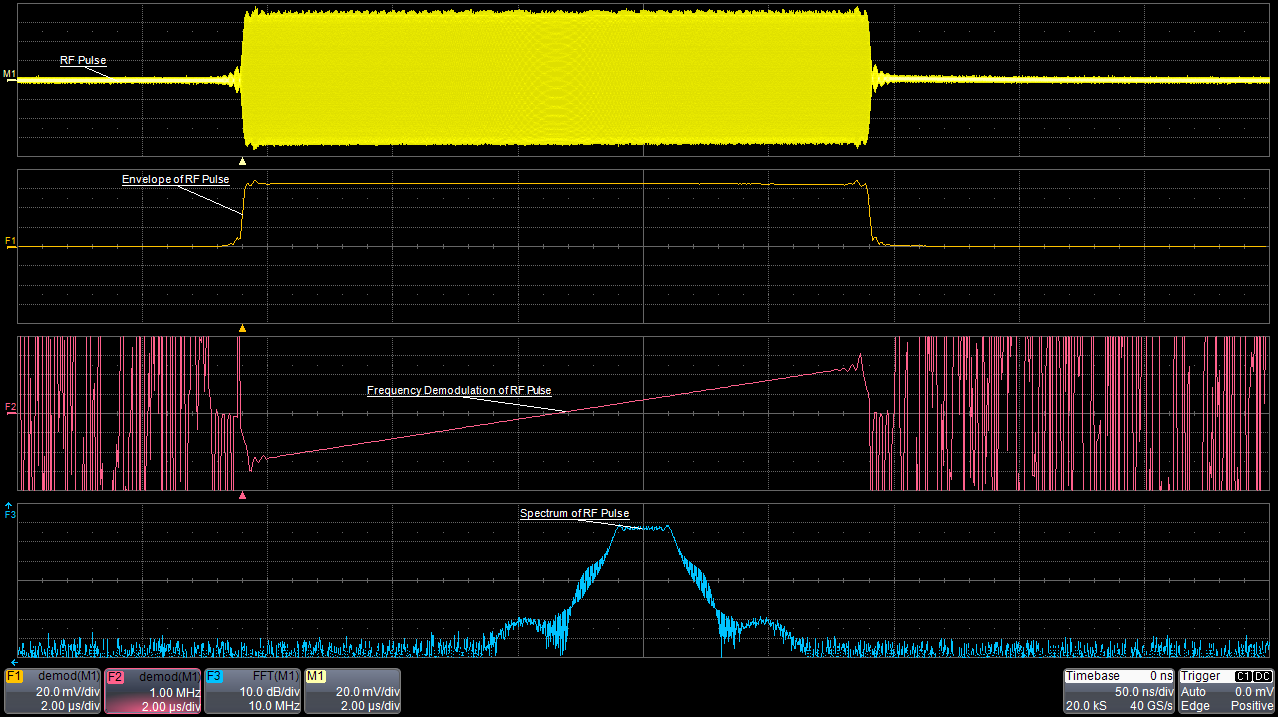 |
Рисунок 3. Пример радиолокационного сигнала с частотной модуляцией |
Последний пример - радиолокационный сигнал с линейной частотной модуляцией (рис. 3). Демодулированный сигнал представляет из себя огибающую (осциллограмма F1), которая показывает, что частота модулируется всем импульсом. Частота увеличивается по линейному закону. В этом случае извлекается форма модуляции. Частота демодуляции (осциллограмма F2) показывает частоту как функцию времени, в то время как БПФ (след F3 голубого цвета) показывает значение частоты как магнитуду.
Данные примеры демонстрируют, как с помощью программного пакета математики можно исследовать радиолокационный сигнал. В дальнейшем мы продолжим разбираться в других аспектах исследования сложных радиочастотных сигналов при помощи математических функций.
Автор: Teledyne LeCroy, перевод с англ. Карданец С.Г. ЗАО «ПриСТ»
Дата публикации: 01.02.2016
У нас представлены товары лучших производителей
ПРИСТ предлагает оптимальные решения измерительных задач.
У нас вы можете купить осциллограф, источник питания, генератор сигналов, анализатор спектра, калибратор, мультиметр, токовые клещи, поверить средства измерения или откалибровать их. Также мы поставляем паяльно-ремонтное оборудование, антистатический инструмент, промышленную мебель. Мы имеем прямые контракты с крупнейшими мировыми производителями измерительного оборудования, благодаря этому можем подобрать то оборудование, которое решит Ваши задачи. Имея большой опыт, мы можем рекомендовать продукцию следующих торговых марок:
Внимание! Отсутствие ошибок и опечаток не гарантируется. В технические характеристики средств измерений неутвержденного типа производителем могут быть внесены изменения без предварительного уведомления. Соответствие важных параметров требует уточнения. Полные технические характеристики предоставляются по отдельному запросу. Нашли ошибку? Выделите мышкой и нажмите Ctrl+Enter.